Well, first, let's explain what a domain and range is A domain is the set of argument values (or "input") in which the function is defined So, for example for a function #g(x) = sqrt(x)#, the domain will be all nonnegative real numbers, or #x >= 0# For this function #f(x)#, we see that the function has no square roots, fractions, or logarithmic functions that would be undefined forFirst week only $499!The Domain and Range of a Function The domain of a function is the set of values for the variable in which the function is defined or real On the
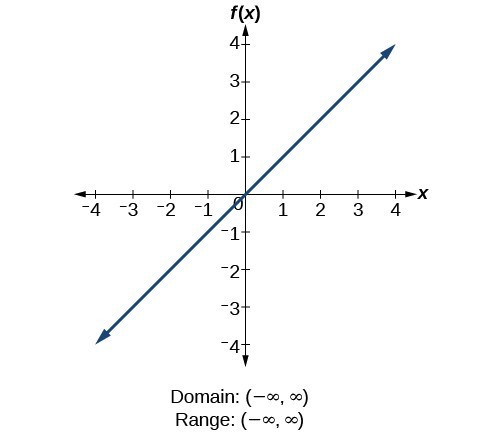
Find Domains And Ranges Of The Toolkit Functions College Algebra
F(x)=log x domain and range
F(x)=log x domain and range- Find the domain and range of the function f(x) = (x2 9)/(x 3) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries For instance, f (x) = The domain is simply the denominator set equal to 0, {xl x≠3} However, range is found by solving for (isolating x to one side) and setting the denominator equal to zero x = So range is {xl x≠0} This is a systematic method that I



Problem 9 Let F X 2 3x4 On The Largest Domain For Which The Formula Makes Sense A Find The Domain And Range Of F X Then Sketch The Graph Course Hero
Solution For The domain and range of y =f(x)= \cos (\log x) are Solution For The domain and range of y =f(x)= \cos (\log x) are Become a Tutor Blog Cbse Question Bank Pdfs Micro Class Download App Class 11 Math All topics Relations and Functions II 508 150 The domainAlgebra Find the Domain and Range f (x) = log base b of x f (x) = logb (x) f (x) = log b (x) Set the base in logb (x) log b (x) greater than 0 0 to find where the expression is definedVerified by Toppr f(x)= x−5 For f(x) to be defined, the term under the Squareroot should be greater than or equal to zero x−5≥0 x≥5 So, the domain is 5,∞) Now, for x−5≥0 x−5
F(x) = 1/x^2 Q 6Chelsea has been offered two jobs Her pay rate at either job will be determined by how well sheThis is a quadratic function There are no rational or radical expressions, so there is nothing that will restrict the domain Any real number can be used for x to get a meaningful output Because the coefficient of x 2 is negative, it will open downward With quadratic functions, remember that there is either aDomain R Range Z The graph of the greatest integer function is shown in figure Greatest integer function Properties of Greatest Integer Function If n is an integer and x is a real number between n and n 1, then (i) n = n (ii) x k = x k, for any integer k
All these are real values Here value of domain (x) can be any real number Hence, Domain = R (All real numbers) We note that that Range f (x) is 0 or negative numbers, Hence, Range = (−∞, 0 Ex 23, 2 Find the domain and range of the following real function (ii) f (x) = √ ((9 −x^2)) It is given that the function is a real functionF(x 1) = 3(x 1) 4 = 3x 7 Domain and Range The domain of a function is the set of values which you are allowed to put into the function (so all of the values that x can take) The range of the function is the set of all values that the function can take, in other words all of the possible values of y when y = f(x)Given f (x) = 2 − ∣ x − 5 ∣ Domain of f (x) is defined for all real values of x Since, ∣ x − 5 ∣ ≥ 0 − ∣ x − 5 ∣ ≤ 0 2 − ∣ x − 5 ∣ ≤ 2 f (x) ≤ 2 Hence, range of f (x) is (− ∞, 2
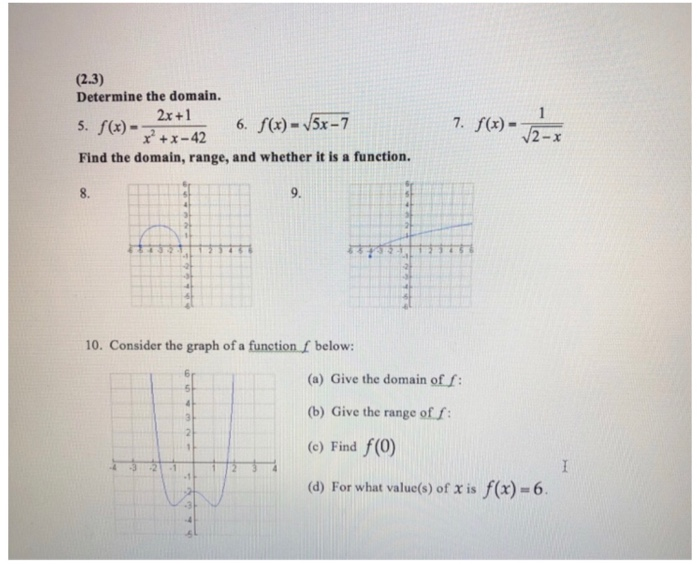



2 3 Determine The Domain 5 F X 6 F X 5x 7 Chegg Com




This Worksheet Has Four Graphs Giving Students Practice In Finding The Domain Range Relative Maximum Relative Minimum Math School School Algebra Precalculus
A function would have at least two sets, and it can either be the domain or range Earlier in the introduction, these are The set of all possible input values is the domain The set of all possible output values is the rangeDomain and range graph The graph of f(x)=x2 f ( x) = x 2 (red) has the same domain (input values) as the graph of f(x)=− 1 12x3 f ( x) = − 1 12 x 3 (blue) since all real numbers can be input values However, the range of the red graph is restricted to only f(x)≥0 f ( x) ≥ 0, or y y values above or equal to 0 0For the cubic function latexf\left(x\right)={x}^{3}/latex, the domain is all real numbers because the horizontal extent of the graph is the whole real number line The same applies to the vertical extent of the graph, so the domain and range include all real numbers



1



1
The range of f (x) is 0,∞), which is all nonnegative real numbers In the same vein what are the domain and range of f/x equals?So, Domain (f) = x ∈ R Range of ( f ) We know that ∣ x ∣ is always positive So, if a positive quantity is being subtracted from 1 then for all other values of ∣ x − 2 ∣ except 0 , 1 y will be negative and maximum value will be when ∣ x − 2 ∣ = 0 then y = 1How to Find the Domain and Range of f(x, y) = ln(xy 2)If you enjoyed this video please consider liking, sharing, and subscribingYou can also help support




L1 Functions Domain Amp Range




What Are The Domain And Range Of F X 1 5 X Brainly Com
Write the Domain and Range of the Function F ( X ) = X − 2 2 − X CBSE CBSE (Commerce) Class 11 Textbook Solutions 8184 Important Solutions 14 Question Bank Solutions 7221 Concept Notes & Videos 365 Syllabus Advertisement Remove all ads Write the Domain and Range of the Function F ( X ) = X − 2 2 − X Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeRange The out comes or values that we get for y is known as range Domain for given function f (x) = x 3 For any real values of x, f (x) will give defined values Hence the domain is R Since we have absolute sign, we must get only positive values by applying any positive and negative values for x in the given function




Finding Domain And Range




Introduction To Function Domain And Range Mohd Noor
Range {yly> 2} domain {x x is a real number}; What are the domain and range of f(x) = (1/6)^x 2?Range {yly>0} domain {x\x> 1/6);



How To Find The Domain Range And Roots Of Polynomials And Rational Functions Universalclass
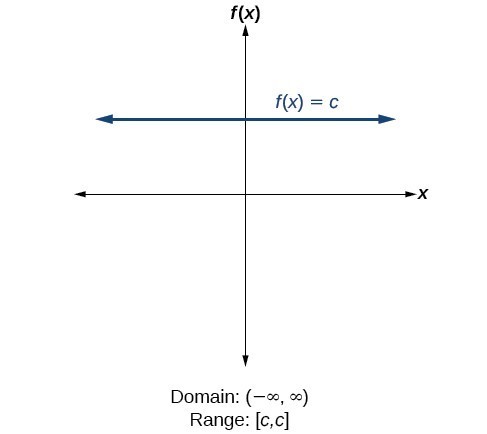



Find Domains And Ranges Of The Toolkit Functions College Algebra
What are the domain and range of the realvalued function f(x) = −3x 2 6x 1?Since, f (x) is defined for x ∈ R, the domain of f is R It can be observed that the range of f ( x ) = − ∣ x ∣ is all real numbers except positive real numbers Therefore, the range of f is ( − ∞ , 0Figure 3 Domain and range of a function and its inverse When a function has no inverse function, it is possible to create a new function where that new function on a limited domain does have an inverse function For example, the inverse of f ( x) = x \displaystyle f\left (x\right)=\sqrt {x} f (x
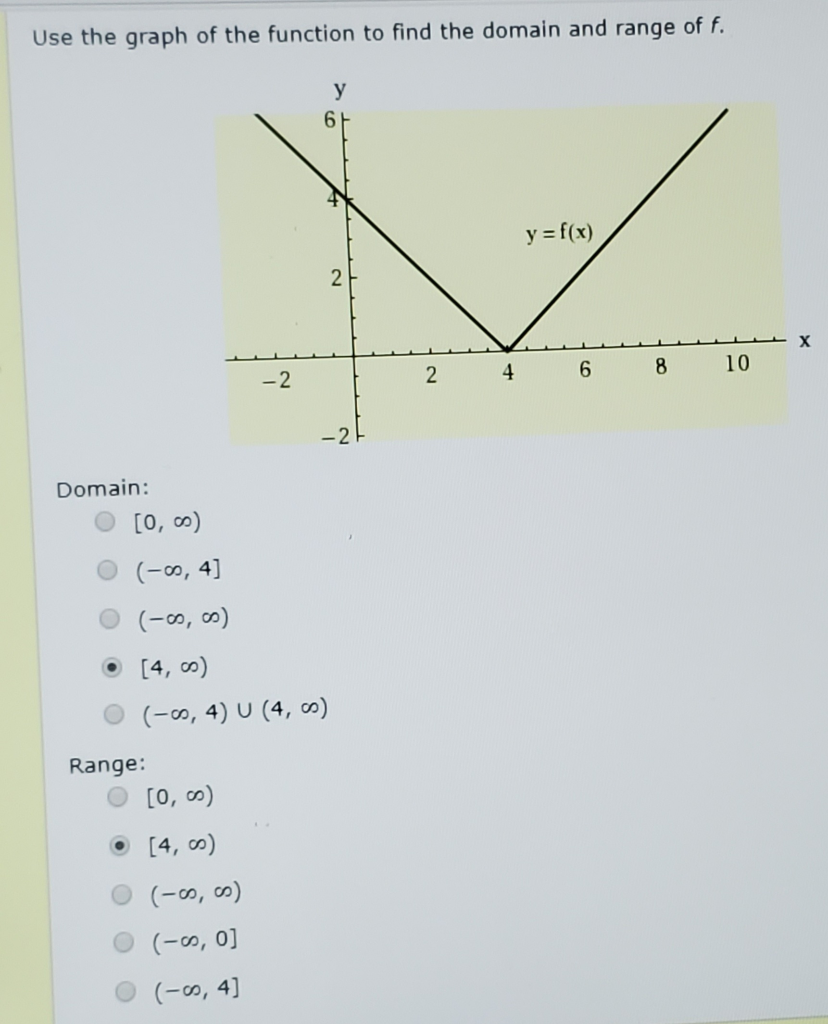



Use The Graph Of The Function To Find The Domain And Chegg Com




Find The Domain And Range Of F X X 1 Youtube
See Answer Check out a sample Q&A here Given f (x) = 1/√x−5 To find the domain and range of function Explanation So, the domain of a function consists of all the first elements of all the ordered pairs, ie, x, so we have to find the values of x to get the required domain Given, f (x) = 1/√x−5 Now for real value of x5≠0 and x5>0 ⇒ x≠5 and x>5 Hence the domain of f = (5, ∞)Domain and Range Function Notation f(x)
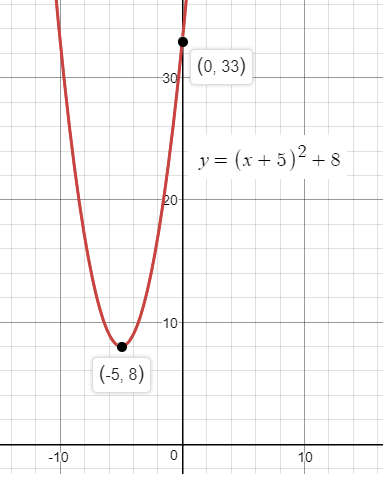



How Do You Find The Domain And Range Of F X X 5 2 8 Socratic




Domain And Range Of Quadratic Functions Video Khan Academy
Arrow_forward Question View transcribed image text fullscreen Expand check_circle Expert Answer Want to see the stepbystep answer? Given f(x) = √x 1 To find the domain and range of function Explanation So the domain of a function consists of all the first elements of all the ordered pairs, ie, x, so we have to find the values of x to get the required domain Given, f(x) = √x 1 Now for real value of x1≥0 ⇒ x≥1 Hence the domain of f = 1, ∞) And the range of a function consists of all the secondTwo ways in which the domain and range of a function can be written are interval notation and set notation Interval notation When using interval notation, domain and range are written as intervals of values For f(x) = x 2, the domain in interval notation is D (∞, ∞)



Http Www Lcps Org Cms Lib4 Va Centricity Domain 1445 Alg 2 ii 7 function review domain range flips pdf Pdf



Domain Range Power
Find the Domain and Range f (x)=x^2 f (x) = x2 f ( x) = x 2 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x xFind the Domain and Range f (x)=x^3 f (x) = x3 f ( x) = x 3 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x xAsk an expert Ask an expert done loading Determine the domain and range of f (x) from its graph Use interval notation Domain Range f (0)= f (x)=3, then x = ______ , ______ Show transcribed image text Expert Answer



Domain And Range Of F X Geogebra
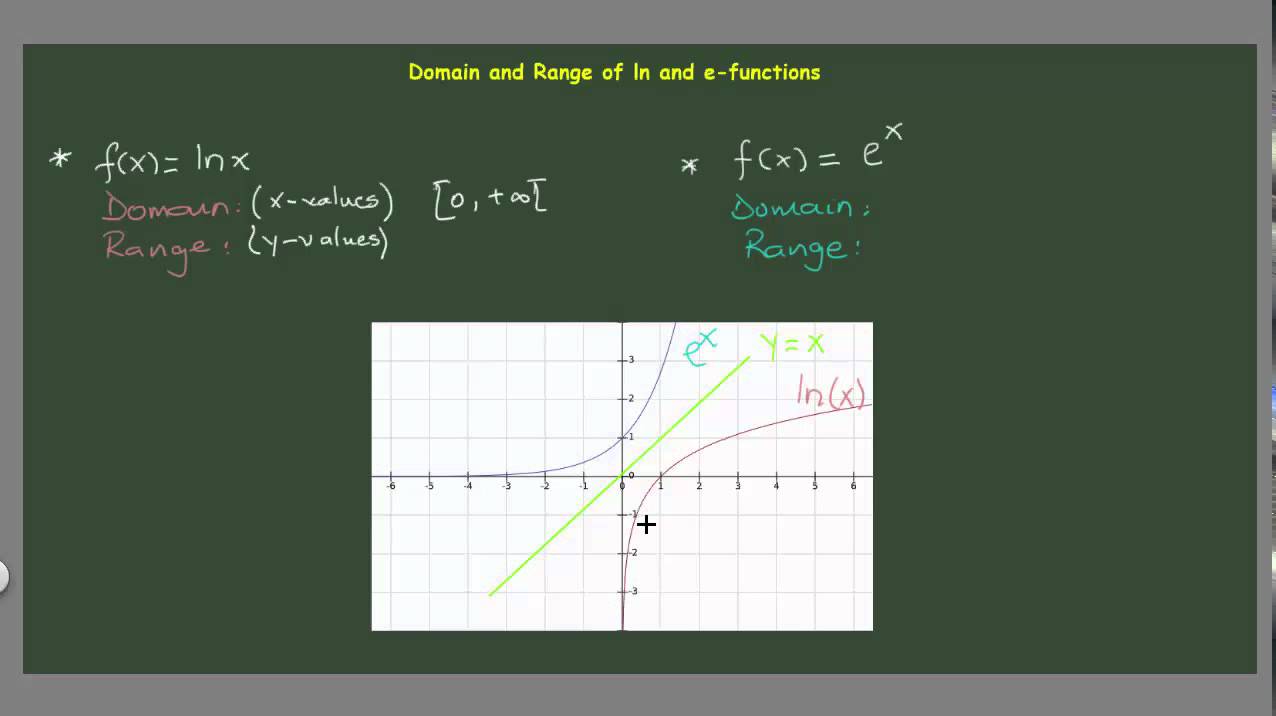



Domain And Range Of Ln And E Functions Youtube
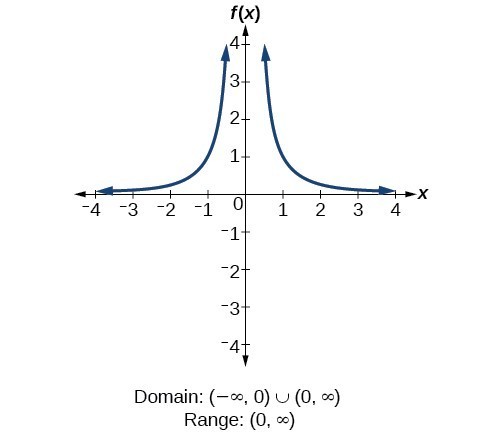
Find the domain and the range of the cube root function, f R → R f(x) = x^1/3 for all x ϵ R Also, draw its graphRational functions f(x) = 1/x have a domain of x ≠ 0 and a range of x ≠ 0 If you have a more complicated form, like f(x) = 1 / (x – 5), you can find the domain and range with the inverse function or a graph See Rational functions Sine functions and cosine functions have a domain of all real numbers and a range of 1 ≤ y ≤ 1 Domain (oo, 0) uu (0, oo) Range (oo, 0) uu (0, oo) Your function is defined for any value of x except the value that will make the denominator equal to zero More specifically, your function 1/x will be undefined for x = 0, which means that its domain will be RR{0}, or




Misc 5 Find Domain And Range Of F X X 1 Class 11




How To Find The Domain And Range Of A Function 14 Steps
The domain of a function, D D, is most commonly defined as the set of values for which a function is defined For example, a function f (x) f (x) that is defined for real values x x in R R has domain R R, and is sometimes said to be "a function over the reals" The set of values to which D D is sent by the function is called the rangeF(x)=ln(x4), domain, range, graph, and its inversePlease checkout my facebook group https//wwwfacebookcom/groups/blackpenredpen/My site for more calculuThe domain of a function f (x) is the set of all values for which the function is defined, and the range of the function is the set of all values that f takes




Find The Domain And Range Of F X Sqrt 16 X 2 Mathematics Stack Exchange




Find The Domain And Range Of The Function F X X 1 X 2 Brainly In
What is the domain and range of f (x) = 1/x?Find the Domain and Range f (x)=5 f (x) = −5 f ( x) = 5 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { xExample 3 Find the domain and range of the function y = log ( x ) − 3 Graph the function on a coordinate planeRemember that when no base is shown, the base is understood to be 10 The graph is nothing but the graph y = log ( x ) translated 3 units down The function is defined for only positive real numbers




Library Of Functions Alg 3 Flashcards Quizlet
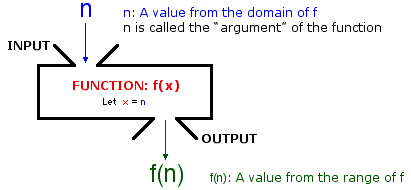



Function
Determine the domain and range for the relation = {(x, y)\x is the sister of y} close Start your trial now! For example, the function f(x) = − 1 √x has the set of all positive real numbers as its domain but the set of all negative real numbers as its rangeIntro to Functions When a Relation is a function?
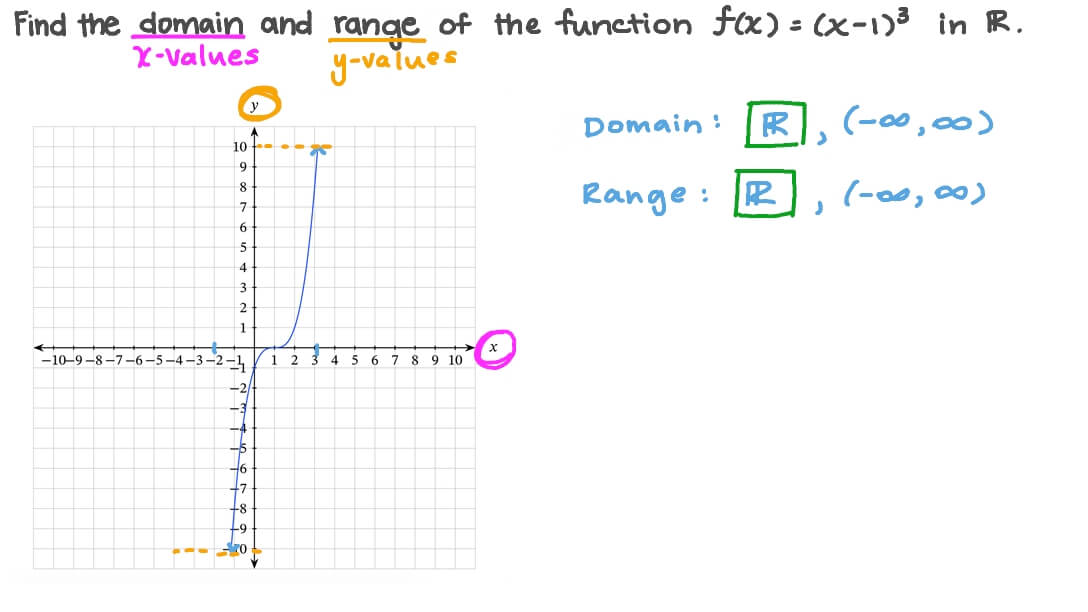



Question Video Finding The Domain And Range Of A Cubic Function Given Its Graph Nagwa
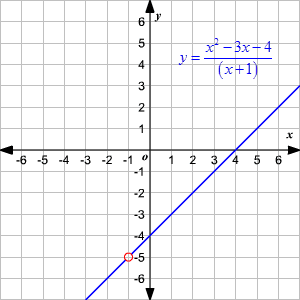



Domain And Range Of Rational Functions
Domain ( oo,3)uu(3, oo) Range (oo,6)uu(6, oo) If you factor the numerator, you can see that you will have terms that cancel out ((x3)(x3))/(x3)=x3 therefore f(x)=x3 with a hole at x=3 So the domain is all real numbers except for x=3 aka (oo,3)uu(3, oo) Plug in three for x to find out where the range doesn't exist y=6 So, the range is all real numbers except for y=6 Solution for what is the domain and range?Find the Domain and Range f (x)=x f (x) = x f ( x) = x The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x x
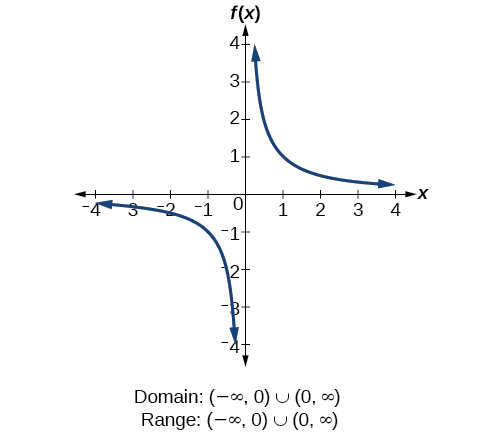



3 3 Domain And Range Mathematics Libretexts



Find The Domain And Range Of The Following Real Functions I F X X Ii F X 9 X 2 Sarthaks Econnect Largest Online Education Community
The given real function is f (x) = x − 1 It can be seen that x − 1 is defined for (x − 1) ≥ 0 ie, f (x) = (x − 1) is defined for x ≥ 1 Therefore the domain of f is the set of all real numbers greater than or equal to 1 ie, the domain of f = 1, ∞)Hence, for the trigonometric functions f (x)= sin x and f (x)= cos x, the domain will consist of the entire set of real numbers, as they are defined for all the real numbers The range of f (x) = sin x and f (x)= cos x will lie from 1 to 1, including both 1 and 1, ie 1 ≤ sin x ≤1
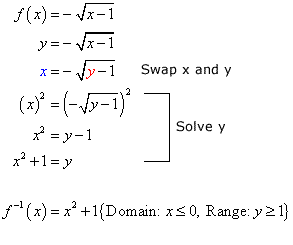



Inverse Of Square Root Function Chilimath



Q Tbn And9gcqpama6tqgin Iutakqatcksftftyjylbbujdpmxcrct Ee Usqp Cau
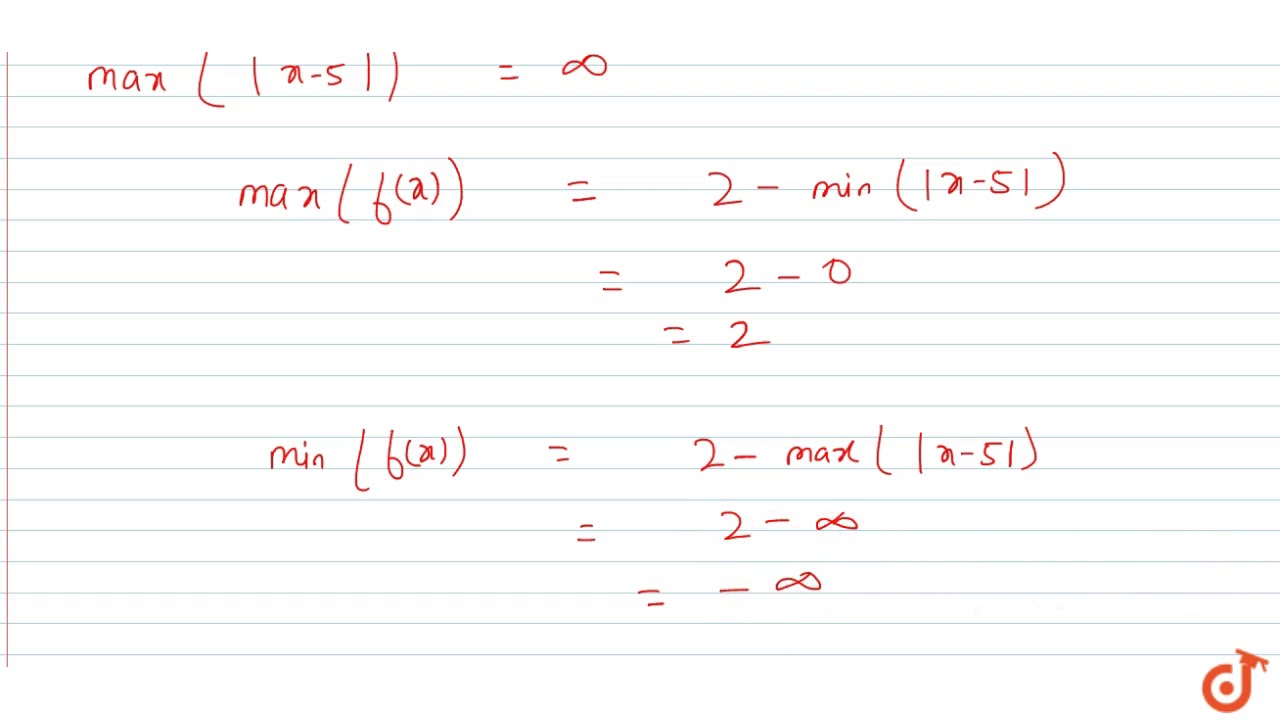



The Domain And Range Of The Function F Given By F X 2 X 5 Is Youtube




Section 1 5 Combinations Of Functions Ppt Download



For The Function F X X 2 5 Find The Domain And Range Enotes Com
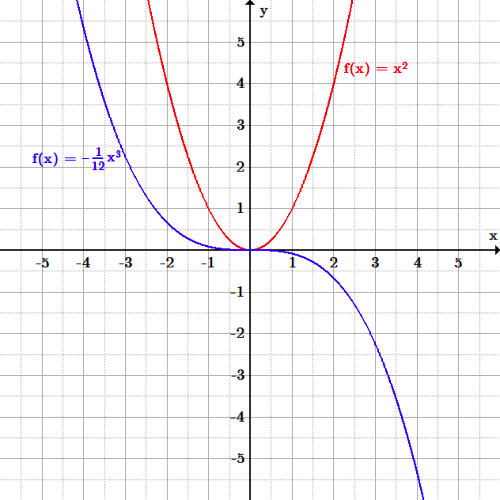



Domain And Range Boundless Algebra
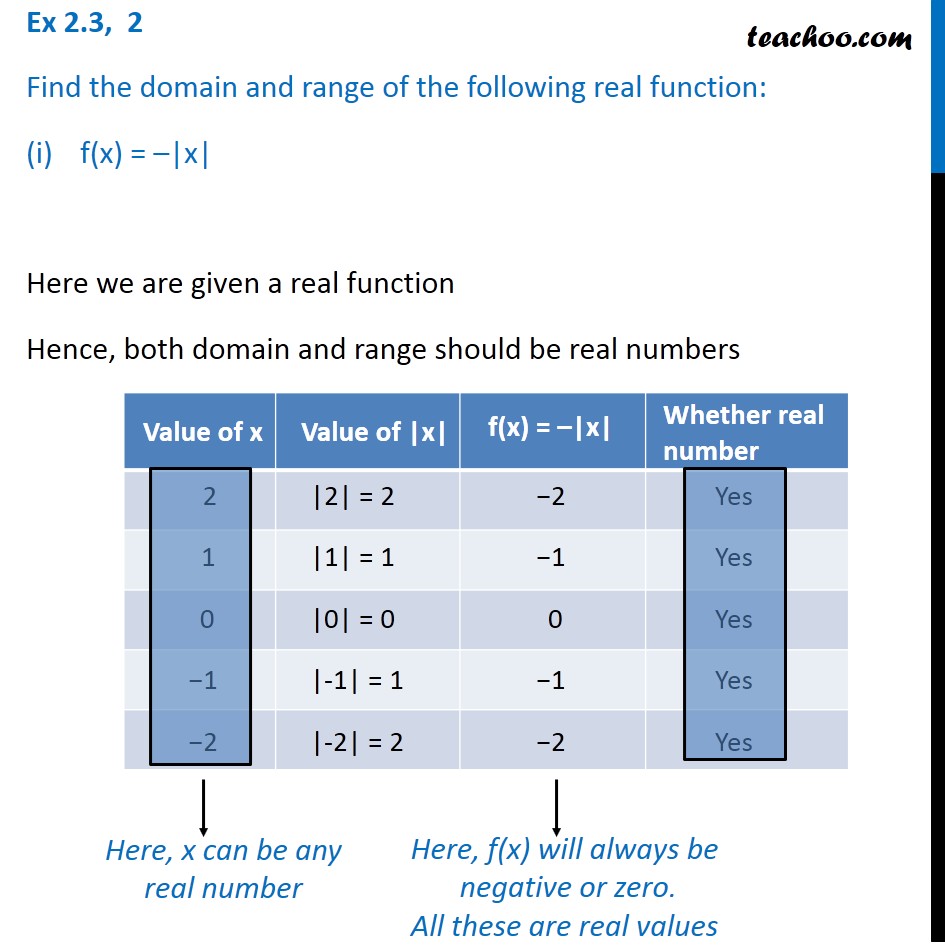



Ex 2 3 2 Find The Domain And Range Of The Function F X X




Find The Domain And Range Of The Real Function Fx 1 1 X 2 Brainly In



What Is The Domain And Range Of Tan X Quora




Domain And Range Of Functions



Http Fsw01 c Cuny Edu Luis Fernandez01 Web Teaching Classes Math30 Nikos 30sp10 Funex Pdf




Find The Domain And Range Of The Function F X 2 X 5




Find The Domain And Range Of F X Sqrt 16 X 2 Mathematics Stack Exchange
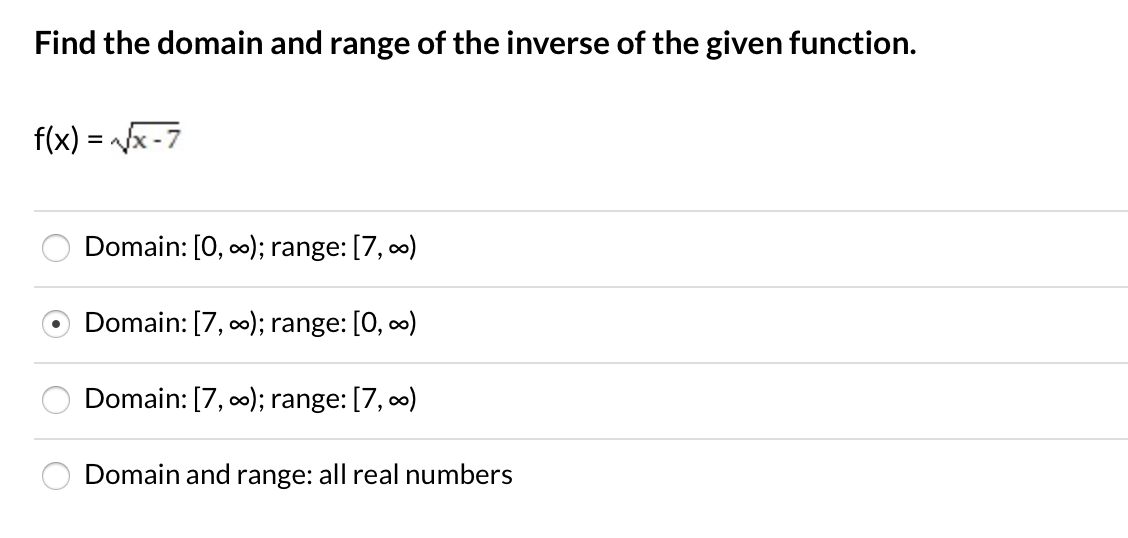



Answered Find The Domain And Range Of The Bartleby



Determine Domain And Range From A Graph College Algebra




Finding The Domain And Range Of A Function In Chegg Com
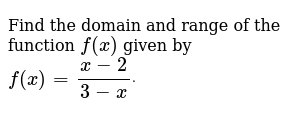



Find The Domain And Range Of The Function F X Given By F X X 2 3 X Dot




Find The Domain And Range Of The Following Real Functions I F X X Ii F X Sqrt 9 X 2




Find The Domain And The Range Of The Function F X X 2 25 X 5 Youtube



What Is The Domain And Range Of F X X X Quora




Domain And Range Of A Function Utrgv



Domain And Range Examples Domain And Range Of Functions



What Is The Domain And Range Of 1 X 3 Quora



Finding Domain And Ranges For Composition Function Physics Forums



Domain And Range Of A Function
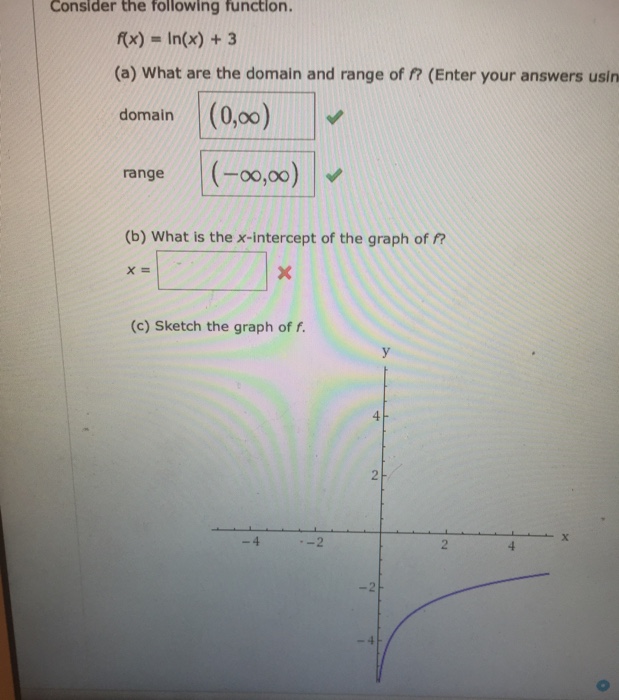



Consider The Following Function F X Ln X 3 Chegg Com



Domain And Range




Find Domain And Range Of Real Functions 1 F X X 2 3 X 2 F X 1 Sqrt X 5 Youtube
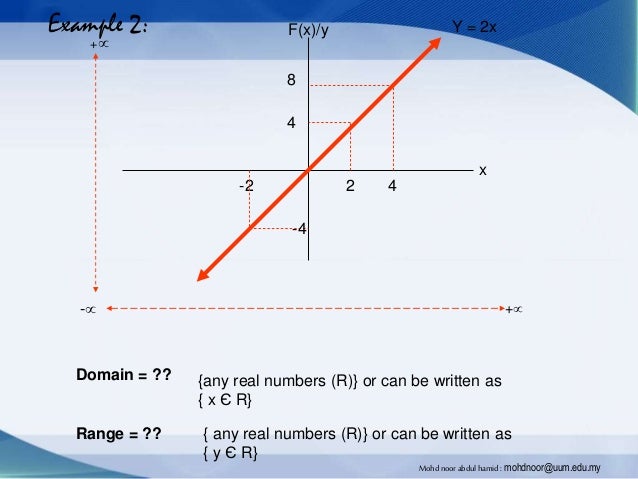



Introduction To Function Domain And Range Mohd Noor




Precalculus The 12 Basic Functions Flashcards Quizlet




Find The Domain And The Range Of The Real Function F X X 3 X 5
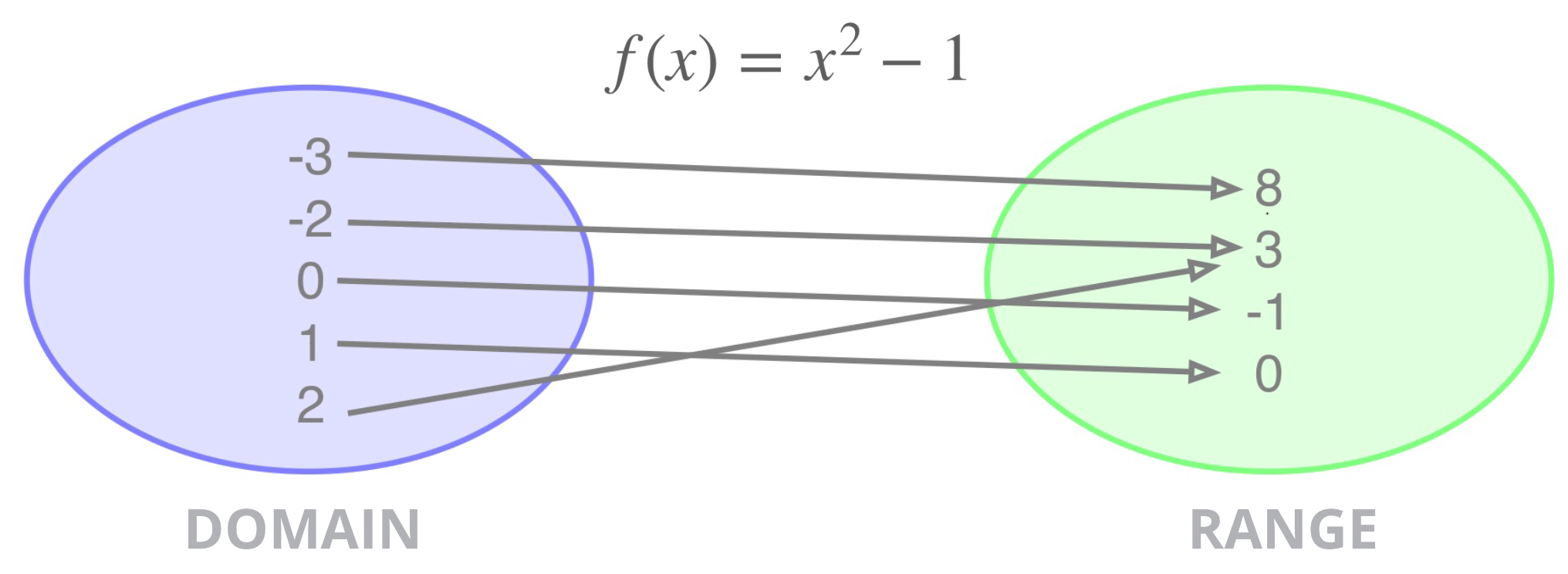



Domain Range A Function
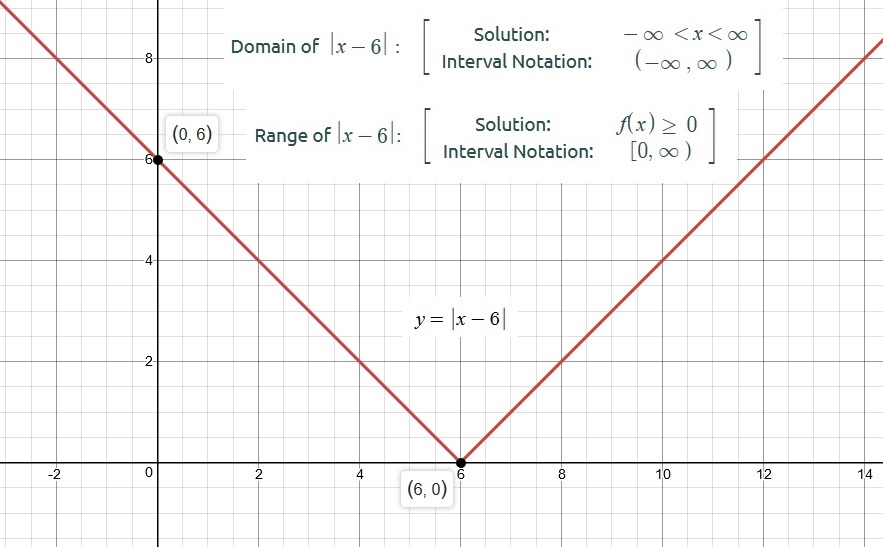



How Do You Find The Domain And Range Of Y X 6 Socratic
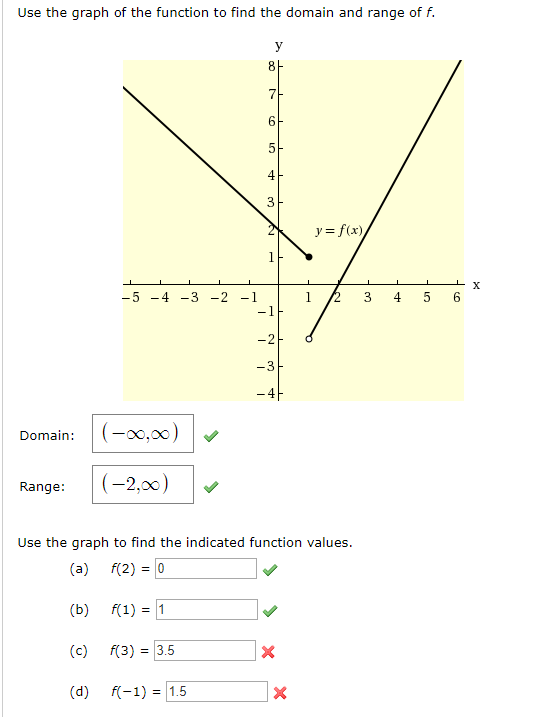



Use The Graph Of The Function To Find The Domain And Chegg Com
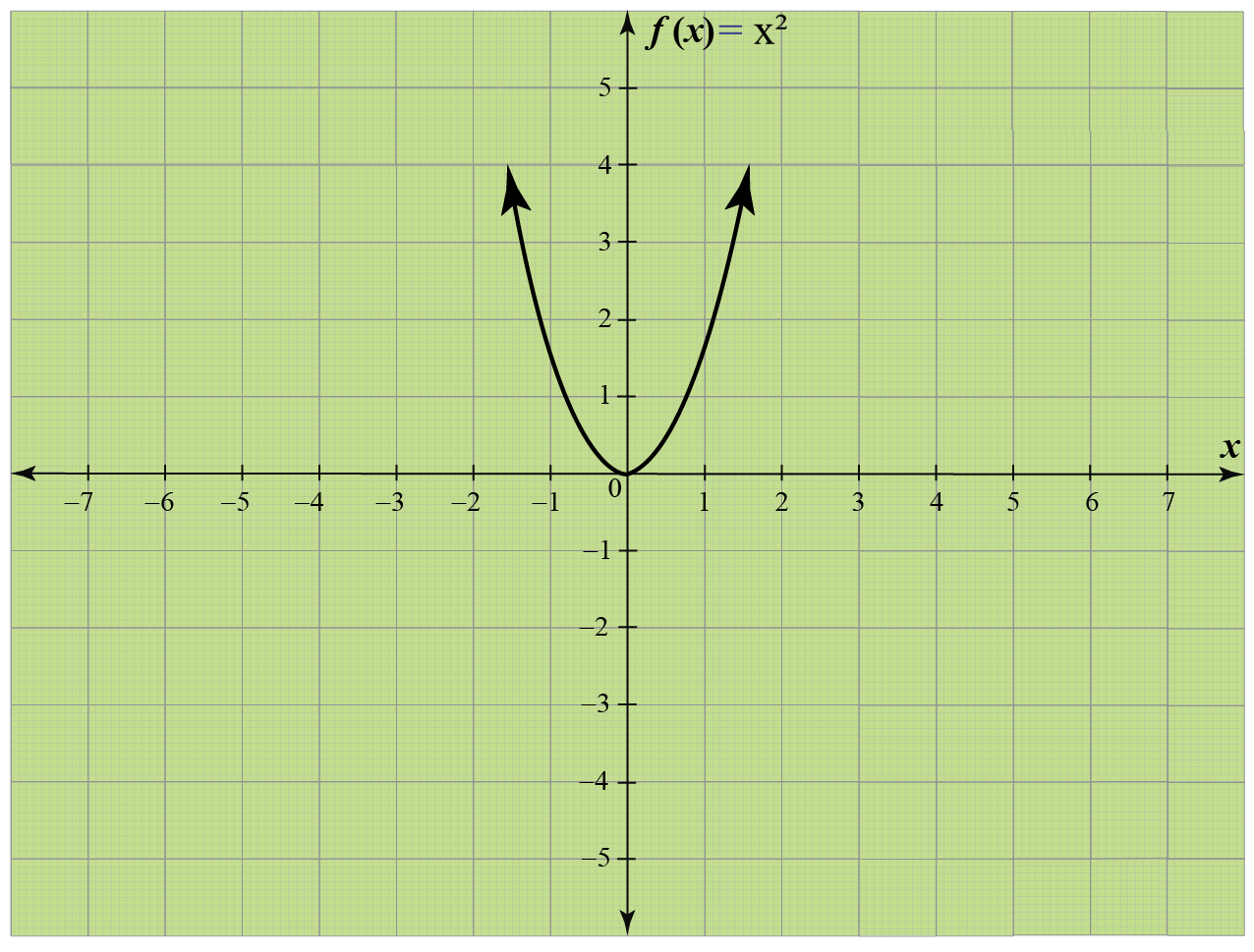



Domain Definition Examples Cuemath



How Do You Find The Domain And Range Of F X X 4 4x 3 3x 2 Socratic
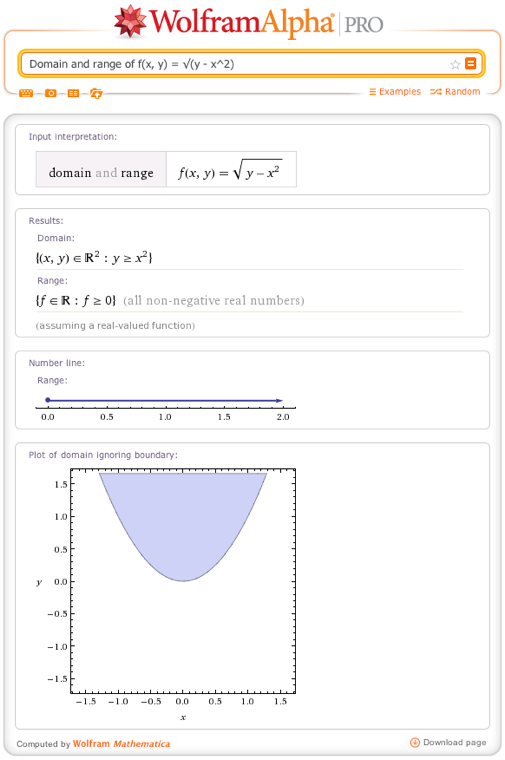



Solve Domain And Range Of A Function With Wolfram Alpha Wolfram Alpha Blog



Domain And Range Of Quadratic Functions Video Khan Academy



Domain And Range Shortcut Rules The Qubits Blog




Domain Range And Codomain



Draw The Graph Of The Function F X X 2 And Write Its Domain And Range Sarthaks Econnect Largest Online Education Community




Domain And Range Calculator Wolfram Alpha




Domain And Range Of F X X 3 X 3 Are Respectively




What Is The Range And The Domain Of F X X2 2x 3 Brainly Com



Problem 9 Let F X 2 3x4 On The Largest Domain For Which The Formula Makes Sense A Find The Domain And Range Of F X Then Sketch The Graph Course Hero
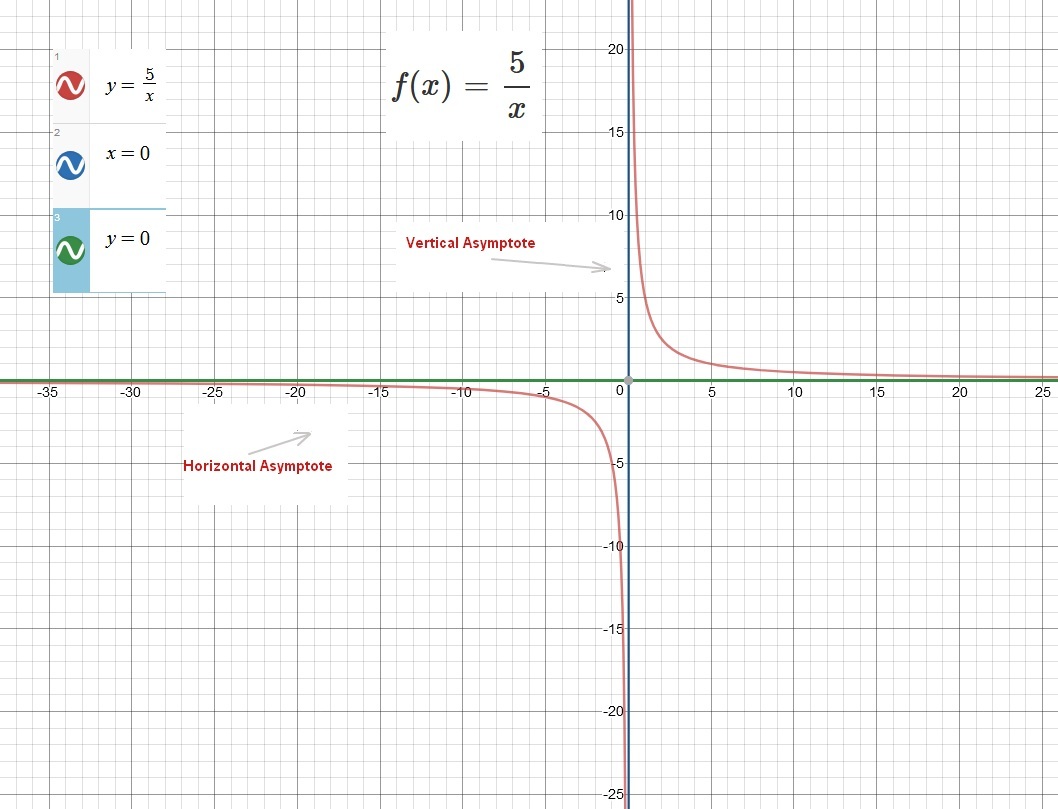



What Is The Domain And Range Of The Function F X 5 X Socratic




Find Domains And Ranges Of The Toolkit Functions College Algebra
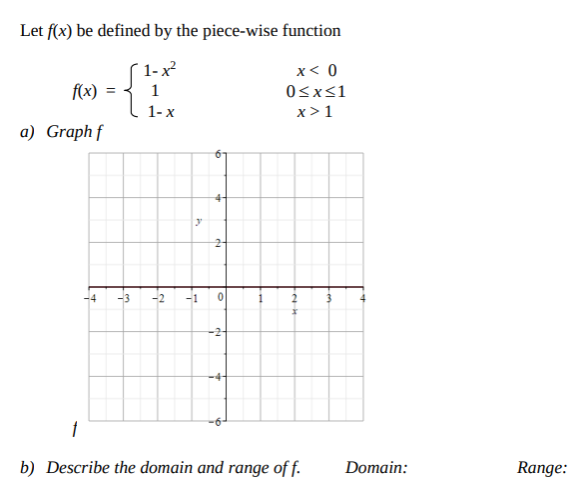



Answered Let F X Be Defined By The Piece Wise Bartleby




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2



Domain Range




Find The Domain And Range Of The Function F X 1 2 Sin3x Youtube




Pc Parent Function Chart




Domain And Range Of Quadratic Functions Video Khan Academy
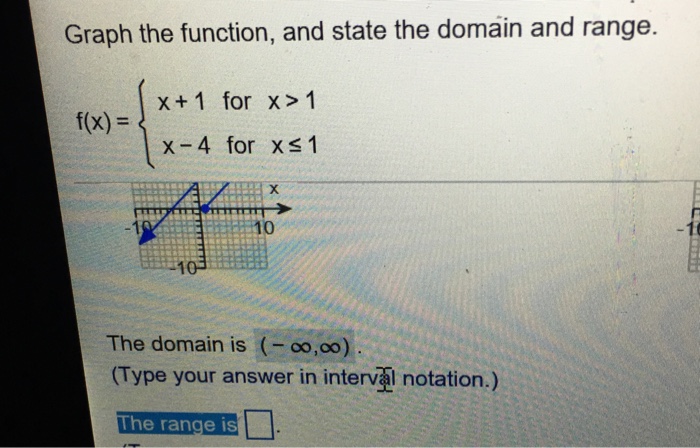



Graph The Function And State The Domain Range F X Chegg Com




F X Log 1 3 H A Domain 0 Range B Domain 0 Homeworklib
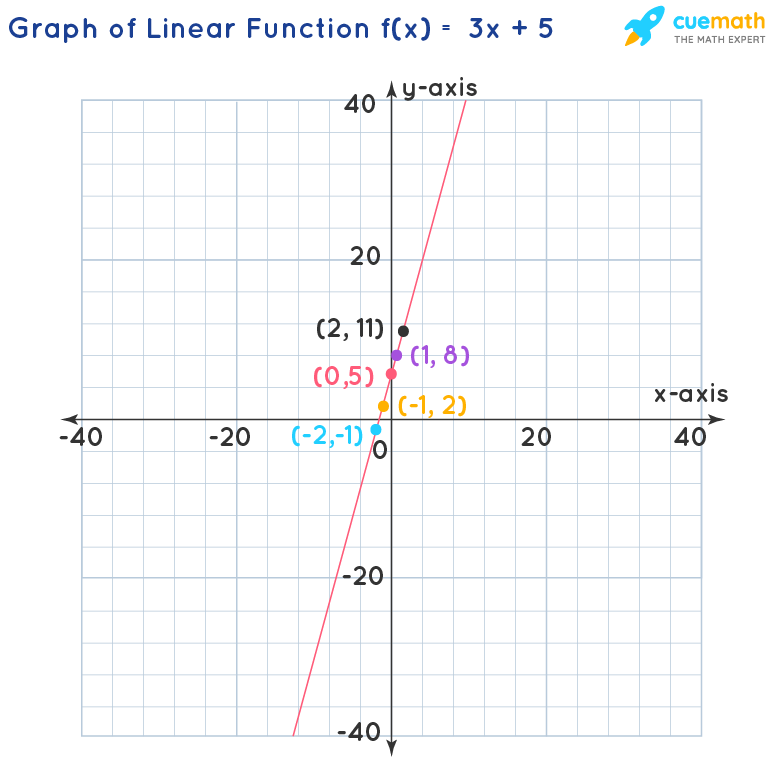



What Are The Domain And Range Of The Function F X 3 X 5 Solved




Finding The Domain Range Of Functions With Inequalities Video Lesson Transcript Study Com




Domain And Range Of Functions




Find The Domain And Range Of The Inverse Of The Given Chegg Com
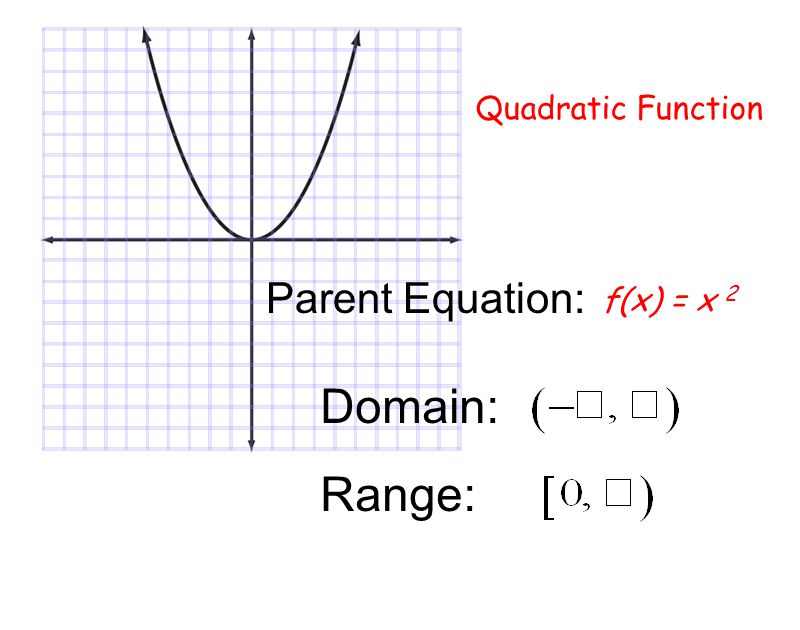



Parent Functions Constant Function Linear Absolute Value Quadratic Ppt Video Online Download




Find The Domain And Range Of The Real Function Defined By F X X 2 1 X 2 Show That F Is Many One
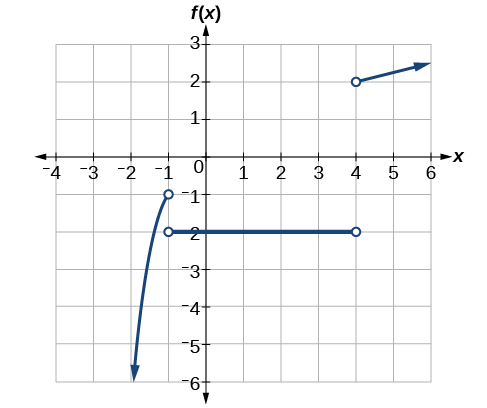



3 3 Domain And Range Mathematics Libretexts



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic




Finding The Domain Range Of Functions With Inequalities Video Lesson Transcript Study Com
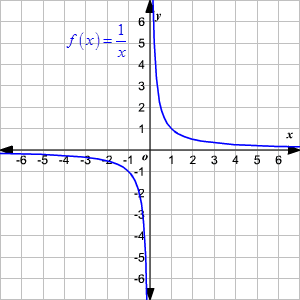



Domain And Range Of Rational Functions




Domain Range




If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are




The Domain And Range Of The Real Function F Defined By F X 4 X X 4 Is



Q Tbn And9gcqnlzmdu7bo39sbnyy8n Qw7ju Qltdhgbmznxvwuughbwlyozz Usqp Cau



Answer In Algebra For Dani Wagas
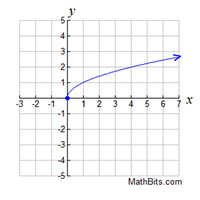



Domain And Range Mathbitsnotebook A1 Ccss Math




Find The Range Of Each Of The Following Functions F X X 3 F X 1 X 2 F X X 4 Youtube




Graph Domain And Range Of Absolute Value Functions
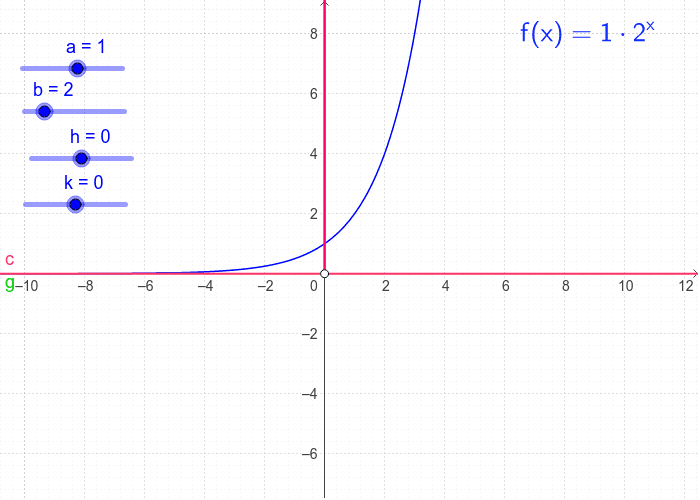



Domain And Range For Exponential Functions Geogebra
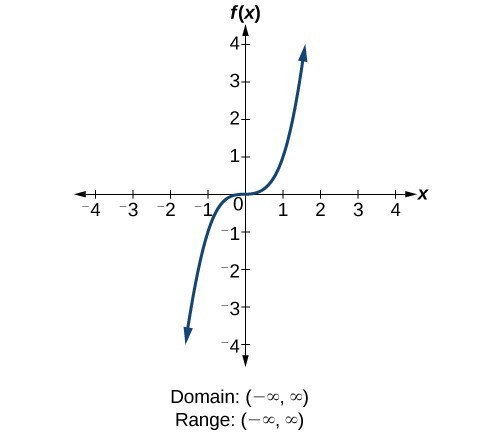



Find Domains And Ranges Of The Toolkit Functions College Algebra
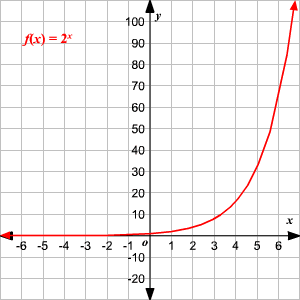



Domain And Range Of Exponential And Logarithmic Functions



0 件のコメント:
コメントを投稿